概念

约 2045 字大约 7 分钟

概念

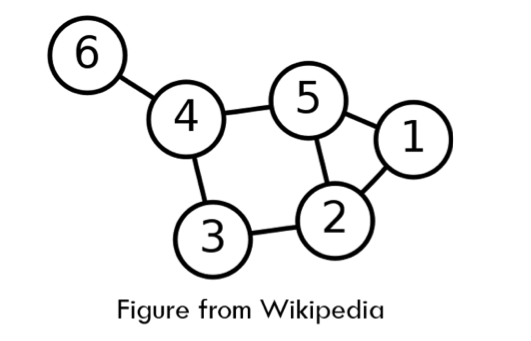
  • 一种抽象的方式表达节点(也叫顶点)和边的连接方式
  • 我们使用1～n标记节点
  • m条边连接一些节点
    • 边可以是单向（有向）或双向
  • 节点和边可以有一些辅助信息

An image

场景

  • 最短路径问题
  • 网络流量问题
  • 匹配问题
  • 2-SAT问题
  • 图着色问题
  • 旅行商问题（TSP）：仍未解决！
  • 其他等等

术语

顶点

顶点，也就是节点

度

  • 顶点的入度，表示有多少条边指向这个顶点
  • 顶点的出度，表示有多少条边是以这个顶点为起点指向其他顶点

邻接

邻接，如果两个顶点被同一个边连接，就称这两个顶点是邻接的。

路径

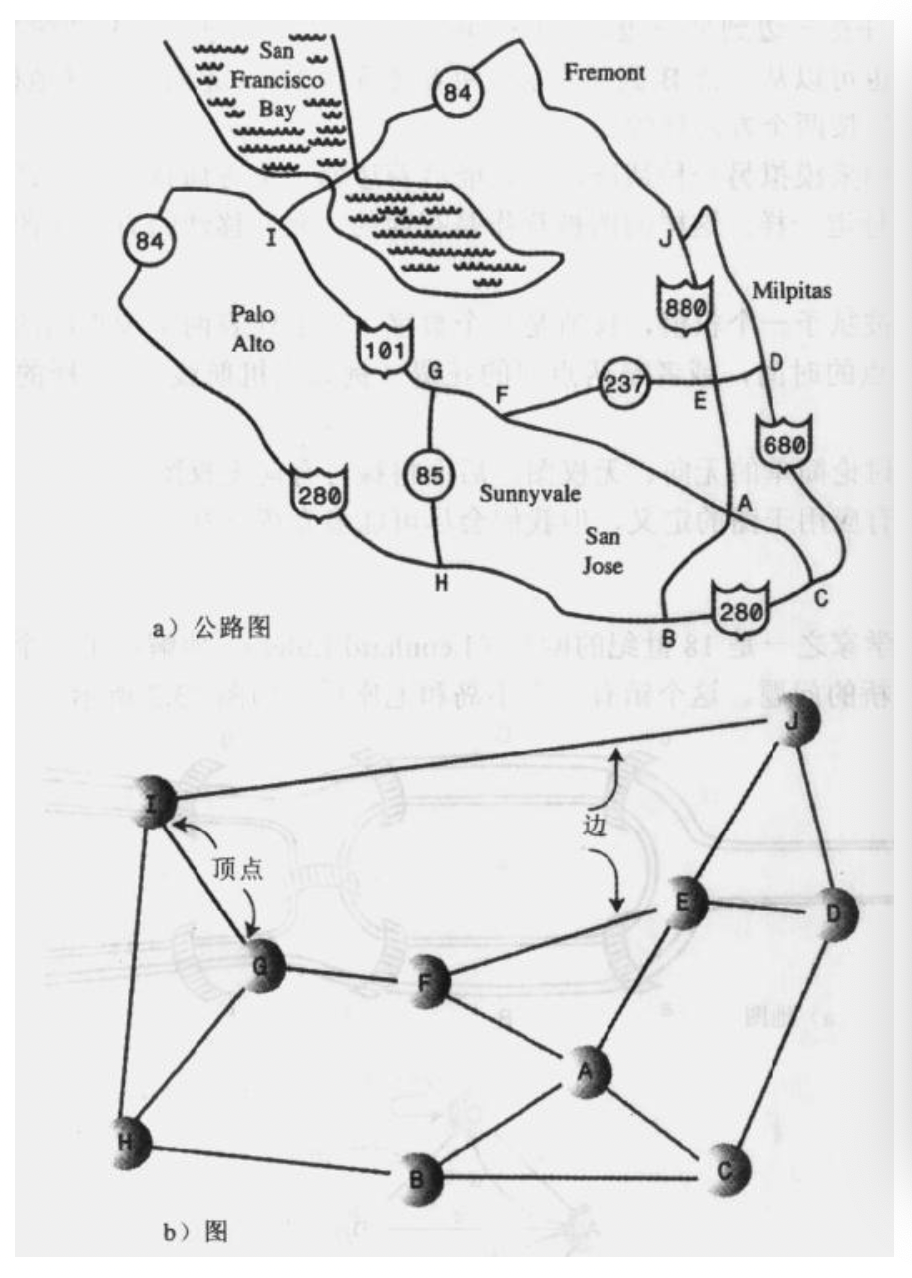
路径，边的序列，例如图中显示了一条从 B 到顶点 J 的路径，这条路径通过了顶点 A 和顶点 E，这条路径叫做 BAEJ。这两个顶点之间还有其他路径，从 B 到 J 的另外一个路径是 BCDJ。

An image

连通图

连通图，如果至少有一条路径可以连接起所有的顶点，那么这个图就被称为连通的。如果没有这样一条路径，就被称为非连通的。

  • 非连通的子图可以是连通的。
  • 连通
  • 非连通
  • 连通无环图
    • 一类最重要的特殊图
      • 许多问题在树上更容易解决
    • 其他等效定义：
      • 连通图需要n-1条边
      • 连通无环图需要n-1条边
      • 每对节点之间只有一条路径
      • 连通无环图增加一条边就会有环
      • 连通图去掉一条边就不再连通
  • 有向连通无环图
    • 有向连通无环图(DAG):名字已经说的很清楚
      • 等价于节点的有序
  • 二部图
    • 节点可以分为两组S和T，这样边只存在于S和T之间（S内或T内没有边）

有向图和无向图

  1. 可以任意一边到另一边，比如公路上没有设定方向，可以从 A->B，B->A
  2. 有向图就像公路上的双向道
  • 设定 A->B , B->A ，等价于无向图
  • 设定 A->B ，则 B->A 等于在单行道上逆行
  • 设定 B->A ，则 A->B 等于在单行道上逆行

有权图和无权图

  • 有权图代表着每一条边都不一样，例如不同距离高速收费不同
  • 无权图代表每条边都是等价的

存储方式

  • 保存集合节点V和集合边E
    • 节点可以存储到数组中
    • 边必须使用其他方式存储
  • 需要支持的操作
    • 检索与特定节点关联的所有边
    • 检验两个节点是否可以连接
  • 使用邻接矩阵或者邻接列表存储边

邻接矩阵

  • 一种简单的方式存储连接信息
    • 检验两个基点是否连接的时间负责度:O(1)
  • 使用 n * n 矩阵 A
    • aija_{ij}= 1 代表从i到j有边
    • aija_{ij}= 0 代表从i到j无边
  • 使用空间O(n2n^2)内存
    • 当n比较小的时候适合使用
    • 稠密图比较适合
ABCD
A0111
B1000
C1000
D1100

邻接表

  • 每一个节点都有向外的边
    • 容易迭代某个顶点上的边
    • 列表长度可变
    • 空间使用O(n + m)

An image

邻接表实现

  1. 使用链表
    1. 内存/时间开销过大
    2. 使用动态分配内存或指针性能好不好
  2. 使用矢量数组
    1. 易于编码，没有内存问题
    2. 但是很慢
  3. 使用数组(!)
    1. 假定总边是知道的
    2. 速度非常快，内存效率也很高

邻接表数组优化

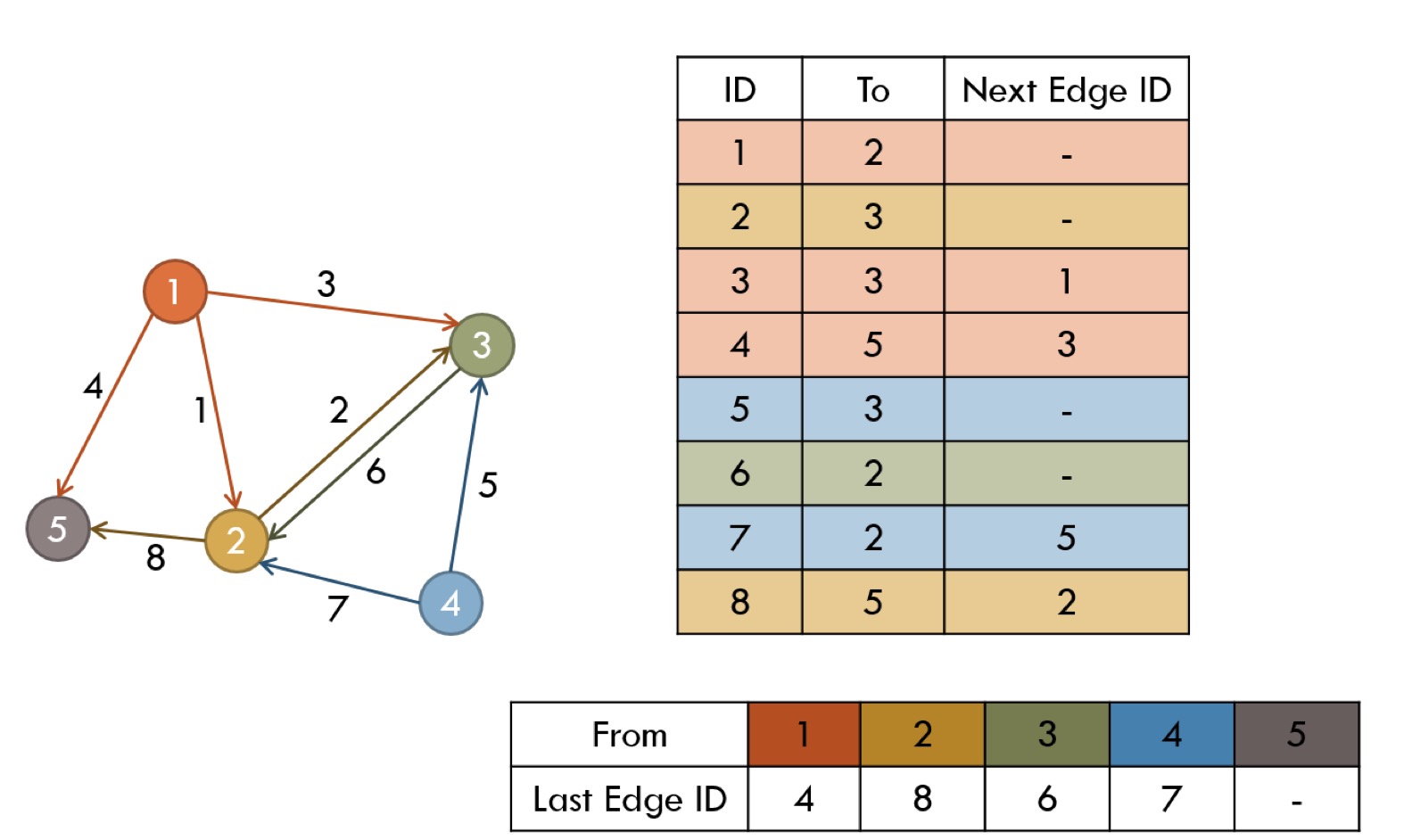
An image

邻接表数组实现

  • 使用两个数组，并且数组E的长度问m，数组LE的长度为n
    • E包含所有的边
    • LE包含开始的顶点和边列表
  • 对于数组全部初始化初始化LE[i]= -1
    • LE[i]=0 如果数组是1索引也可以
  • 插入一个边从u->v，并使用ID=k
    • E[k].to = v
    • E[k].nextID = LE[u]
    • LE[u] = k
  • 迭代从u开始的所有边
for(ID = LE[u]; ID != -1; ID = E[ID].nextID)
       // E[ID] is an edge starting from u
  • 一旦构建，就很难修改边
    • 图必须是静态的
    • 增加边很难

代码

邻接矩阵代码

  1. 编写顶点
type Vertex struct {
  // 这里是数据，后面可以转换成对象
  label rune
  // 是否访问过，在遍历的时候很有用
  wasVisited bool
}

func newVertex(label rune) *Vertex {
  return &Vertex{label: label, wasVisited: false}
}
  1. 图结构和初始化图
const MaxVertex int = 20
const LINK int = 1

type Graph struct {
  vertexList []*Vertex
  adjMat     [][]int
  nVertex    int
}

func newGraph() *Graph {
  return &Graph{
    vertexList: make([]*Vertex, MaxVertex),
    adjMat:     make([][]int, MaxVertex, MaxVertex),
    nVertex:    0,
  }
}
  1. 新增顶点
func (g *Graph) addVertex(label rune) {
  g.nVertex++
  g.vertexList[g.nVertex] = newVertex(label)
}
  1. 连接边
func (g *Graph) addEdge(start, end int) {
  g.adjMat[start][end] = LINK
  g.adjMat[end][start] = LINK
}

邻接表代码

提示

代码来源于算法4open in new window，源码使用邻接表方式编写。

  1. 数据表现
 *  % java Graph tinyG.txt
 *  13 vertices, 13 edges
 *  0: 6 2 1 5
 *  1: 0
 *  2: 0
 *  3: 5 4
 *  4: 5 6 3
 *  5: 3 4 0
 *  6: 0 4
 *  7: 8
 *  8: 7
 *  9: 11 10 12
 *  10: 9
 *  11: 9 12
 *  12: 11 9
  1. 基础代码，后面使用的Bagopen in new window其实也就是List。
public class Bag<Item> implements Iterable<Item> {
  private Node<Item> first;    // beginning of bag
  private int n;               // number of elements in bag

  // helper linked list class
  private static class Node<Item> {
      private Item item;
      private Node<Item> next;
  }

  public Bag() {
      first = null;
      n = 0;
  }

  public boolean isEmpty() {
      return first == null;
  }

  // 数量
  public int size() {
      return n;
  }

  // 增加元素
  public void add(Item item) {
      Node<Item> oldfirst = first;
      first = new Node<Item>();
      first.item = item;
      first.next = oldfirst;
      n++;
  }

  public Iterator<Item> iterator()  {
      return new LinkedIterator(first);
  }
  // 迭代器设计模式
  // an iterator, doesn't implement remove() since it's optional
  private class LinkedIterator implements Iterator<Item> {
      private Node<Item> current;

      public LinkedIterator(Node<Item> first) {
          current = first;
      }

      public boolean hasNext()  { return current != null;                     }
      public void remove()      { throw new UnsupportedOperationException();  }

      public Item next() {
          if (!hasNext()) throw new NoSuchElementException();
          Item item = current.item;
          current = current.next;
          return item;
      }
  }
}
  1. 无向图的顶点命名从0～n（n = V-1)
public class Graph {
  private static final String NEWLINE = System.getProperty("line.separator");
  // 命名从0～n，顶点
  private final int V;
  // 边
  private int E;
  private Bag<Integer>[] adj;
}
  1. 无向图有两个主要的操作
    1. 增加一个边到图中
public void addEdge(int v, int w) {
  validateVertex(v);
  validateVertex(w);
  E++;
  adj[v].add(w);
  adj[w].add(v);
}
  1. 从一个顶点迭代所有相邻的顶点
public Iterable<Integer> adj(int v) {
  validateVertex(v);
  return adj[v];
}
  1. 返回顶点的度
public int degree(int v) {
  validateVertex(v);
  return adj[v].size();
}
  1. 查看顶点数量
/**
* 返回这个图中顶点的数量
* Returns the number of vertices in this graph.
*
* @return the number of vertices in this graph
*/
public int V() {
  return V;
}
  1. 查看边数量
/**
  * Returns the number of edges in this graph.
  *
  * @return the number of edges in this graph
  */
public int E() {
  return E;
}
  1. 初始化图
public Graph(int V) {
  if (V < 0) throw new IllegalArgumentException("Number of vertices must be non-negative");
  this.V = V;
  this.E = 0;
  // 数组长度为V
  adj = (Bag<Integer>[]) new Bag[V];
  // 数组全部初始化
  for (int v = 0; v < V; v++) {
      adj[v] = new Bag<Integer>();
  }
}

public Graph(In in) {
  if (in == null) throw new IllegalArgumentException("argument is null");
  try {
      // 数组数量
      this.V = in.readInt();
      if (V < 0) throw new IllegalArgumentException("number of vertices in a Graph must be non-negative");
      // 初始化
      adj = (Bag<Integer>[]) new Bag[V];
      for (int v = 0; v < V; v++) {
          adj[v] = new Bag<Integer>();
      }
      // 图的边
      int E = in.readInt();
      if (E < 0) throw new IllegalArgumentException("number of edges in a Graph must be non-negative");
      for (int i = 0; i < E; i++) {
          // 连通两个边
          int v = in.readInt();
          int w = in.readInt();
          validateVertex(v);
          validateVertex(w);
          // v w 连通
          addEdge(v, w);
      }
  }
  catch (NoSuchElementException e) {
      throw new IllegalArgumentException("invalid input format in Graph constructor", e);
  }
}

// 原型设计模式，深克隆
public Graph(Graph G) {
  this.V = G.V();
  this.E = G.E();
  if (V < 0) throw new IllegalArgumentException("Number of vertices must be non-negative");

  // 初始化
  // update adjacency lists
  adj = (Bag<Integer>[]) new Bag[V];
  for (int v = 0; v < V; v++) {
      adj[v] = new Bag<Integer>();
  }

  for (int v = 0; v < G.V(); v++) {
      // reverse so that adjacency list is in same order as original
      // 反转原来数据
      Stack<Integer> reverse = new Stack<Integer>();
      for (int w : G.adj[v]) {
          reverse.push(w);
      }
      // 数据增加到bag中
      for (int w : reverse) {
          adj[v].add(w);
      }
  }
}